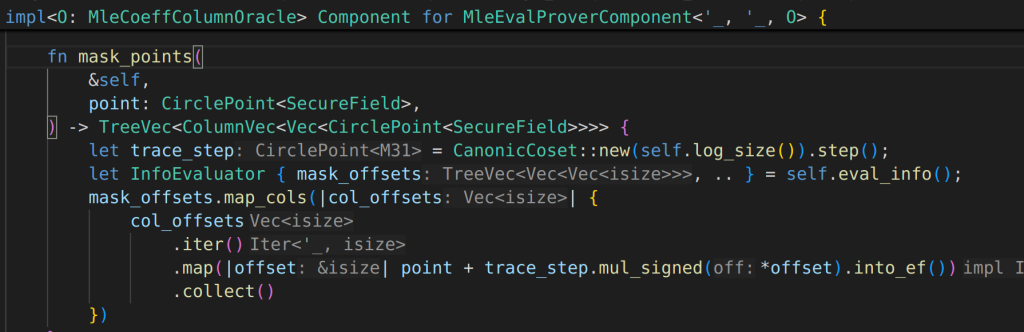
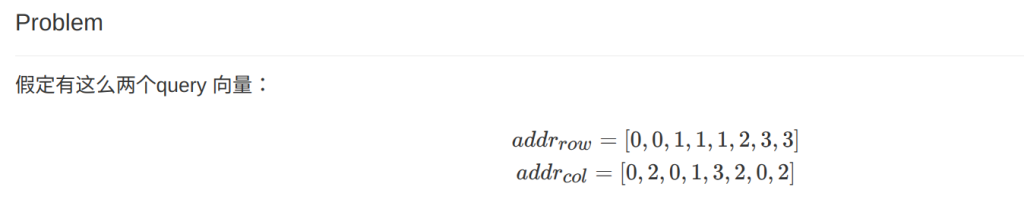shuangcrypto.com - Shuang's Crypto Notes

Notes for bus in stwo

related to this PR

Test case

cargo install --path ./cli-rs

compile with the correct field

powdr-rs compile riscv/tests/riscv_data/keccak -o output --field bb

cargo run --features stwo pil  output/keccak.asm --linker-mode native  -o output --force --field m31  --prove-with stworesult.txt

This can give keccak_opt.pil file with lookup identity, it is native lookup, …

An $O(n)$-sized circuit for evaluating $\widetilde{M}$

talking about this circuit:

notes:

for witness: $row, col, val$ are enough to describe a multilinear extension $\widetilde{M}$

$e_{row}, e_{col}$ should be the evaluations

I need recap on Offline memory checking

let’s follow this post to continue

I think …

Native logup implementation of Stwo backend Powdr -2

following the first post 1

test command

RUST_LOG=stwo=trace cargo test --package powdr-pipeline --test pil --features stwo -- witness_lookup --exact --show-outputresult.txt

Implementation notes

Witness to BaseColumn

witness needs to be transformed into BaseColumns and then use the combine function to get fraction.

in Plonk example, all the witness columns are …

Deep dive to InfoEvaluator of Stwo

The reason I write this is because I saw the verification sample ood points are related to InfoEvalator. InfoEvalator contains this mask or mask offset information which basically embedded the circuit information.

This mask points of MleEvalProverComponent

Start with component built

when a component is buit, it takes a location_allocator, …

Native logup implementation of Stwo backend Powdr

Powdr side:

run test in pipeline (I changed the test so it can include stwo):

#[test]
fn witness_lookup() {
    let f = "pil/witness_lookup.pil";
    let inputs = [3, 5, 2, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7]
        .into_iter()
        .map(GoldilocksField::from)
        .collect::<Vec<_();
    let pipeline = make_prepared_pipeline(f,

…

Bus in different field -1

the goal is to understand the extra cost (witness column) brought by using different field, in the bus part.

start with lookup_via_challenges_range_constraint.asm

use std::convert::fe;
use std::protocols::lookup::lookup;
use std::math::fp2::from_base;
use std::prover::challenge;

machine Main with degree: 8 {

    // Prove a correct decomposition of x into 3-bit limbs
    col fixed x =

…

Spartan 4

previous posts: 1,2, and 3

Overview of spartan paper

summarize again what spartan paper offer:

transparent zksnark for arbitrarily NP statement
sub-linear verification
time optimal prover

sub-linear verification,computation commitment for sparse multilinear polynomials

recall in post 3, the remaining problems:

use extractable polynomial commitment for multiliear polynomial

…

Spartan 3

following the previous posts about spartan: 1 and 2

Chapter 5, A family of NIZKs with succinct interactive argument of knowledge

from post 1 we get a goal to check

$\mathcal{Q}_{io}(\tau)=\sum\limits_{x\in \{0,1\}^s}\mathcal{G}_{io,\tau}(x)=\sum\limits_{x\in \{0,1\}^s}\widetilde{F}_{io}(x)\cdot \widetilde{eq}(\tau,x)=0$

where $\tau$ is a random checking point.

recall we have:

$\widetilde{F}_{io}(x)=\left(\sum\limits_{y\in\{0,1\}^s}\widetilde{A}(x,y)\cdot Z(y)\right)\cdot \left(\sum\limits_{y\in\{0,1\}^s}\widetilde{B}(x,y)\cdot Z(y)\right)$

let’s start …

On my way to review, about lookup –1

Trying to understand from this PR

understanding lookup.asm

let is_first: col = |i| if i == 0 { 1 } else { 0 };

the above line, defines fix column, fix columns are columns known during circuit setup, independent of the what the witness will be. “i” represent the row …

Spartan 2 some basic terminologies

Follow my first post for Spartan

Closed-form expression for evaluating a polynomial

The closed-form expression for evaluating a polynomial $\mathcal{G}(\cdot)$ at $(r_1,…,r_m)\in \mathbb{F}^m$ is

$$\mathcal{G}(r_1,…,r_m)=\sum\limits_{x\in\{0,1\}^m}\mathcal{G}(x)\prod\limits^{m}_{i=1}\underbrace{(r_i\cdot …

Author: shuangcrypto.com