Table of Contents
Traits
- Definition: Traits are a way to define shared behavior in Rust. They define a set of methods that a type must implement in order to fulfill the
Learning new things!
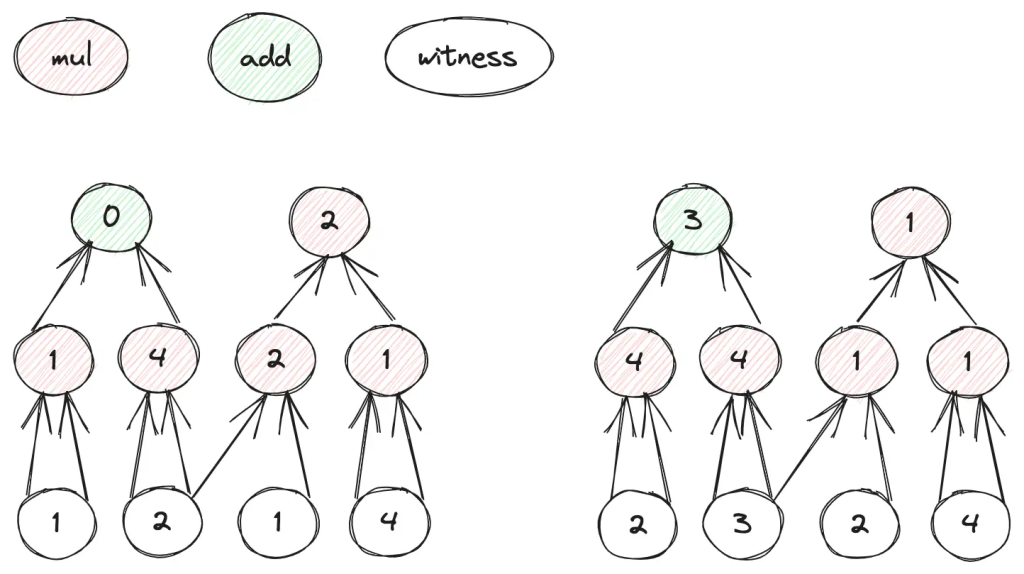
Take example circuit in figure 1, following the Arithmetization described in post, a step by step description of GKR arithmetication of a concrete example.
\(q’\in \{0,1\}^{b_N}\): The index of one of the \(N\) identical copies of the base circuit \(C_0\) within \(C\).…
To understand the attack on Nova, I figure out I need to understand the role of the hash function and the validation check of hash function in Nova, from the first paper where the “cycle of curves” is not introduced, the circuit is illustrated as

to …
After understanding of the folding scheme of relaxed R1CS, of which the key idea is you can “fold” two proofs to be one, with this ability of relaxed R1CS in mind, how can one build a recursive proof from scratch? in this note I will describe several attempts to build …
explain the multipoints opening of Halo 2, I don’t think Halo2 book explain this part clearly, and perhaps, neither my note.
the key, is the homomorphism of the commitment scheme. and combine the evaluation at different points, and combine the different polynomial evaluated at the same points. Later if I …
A user want to send a message from one chain to another chain
resource
https://starkware.co/stark-101
interpolate the trace points into a polynomial in …
how to build zkVM:
Stark can be described in 5 steps in a high level:
$$f(X)=f_E(X^2)+X\cdot f_O(X^2)$$
if we take an intermediate variant \(Y\) to replace the \(X^2\)
With a fixed \(Y\), then \(f(x)\) can be considered as one degree polynomial for \(X\), as
$$f(X)=f_E(Y)+X\cdot f_O(Y)$$
and for a given \(y\), it determineds a unique line (one degree polynomial)
and the …