explain the multipoints opening of Halo 2, I don’t think Halo2 book explain this part clearly, and perhaps, neither my note.
the key, is the homomorphism of the commitment scheme. and combine the evaluation at different points, and combine the different polynomial evaluated at the same points. Later if I got time, I will try to re-write this note…
Table of Contents
Statement
Take the example from Halo2 book:
- Four advice columns \(a,b,c,d\)
- One fixed column \(f\).
- Three custom gates:
- \(a\cdot b \cdot c_{-1}-d =0\)
- \(f_{-1}\cdot c\)=0
- \(f\cdot d\cdot a\)=0
commitment
Transfer the three gates constrains to polynomial constraints

These polynomial constrains are satisfied, which means at domain \(\{w, w^1, …,w^{n-1}\}\), \(gate_0(X), gate_1(X),gate_2(X)\) evaluated to 0. i.e., the polynomial constrain is perfectly divisible by vanishing polynomial.

and then the prover commits to the polynomial (\(y\) is used to combined the polynomials together to be one, the same functionality with \(\alpha\) in plonk)
As the polynomial constraint has degree \(3n-3 (d=3)\), but halo2 only supports committing to polynomials of degree \(n-1\) (this is limited by the inner product argument, the other vector has degree \(n-1\)), so the commitment to \(h(X)\) is splitted.

Opening of the commitment
in KZG commitment, the random point is already “hide” in the reference string, but here, the verifier need to choose a point.
but, one thing confused me a lot is that, KZG and IPA are PCS (polynomial commitment scheme), which has basically two key points: commit to a polynomial, then later show the polynomial’s evaluation at a random point. how these two functions are utilized in these zk proof? this come back one step before we talking about the quotient polynomial \(h(x)\).
we want to verify the polynomial’s evaluation are 0 at the domain, in IPA, that means for all the points in the domain \(w,w^1,…,w^{n-1}\), verifer\prover need to form a vector to do a inner product proof and the inner products are 0:
\(w,w^2,w^3,….w^{n-1}\) for point \(w\)
\({w^2},{w^2}^2,{w^2}^3,….{w^2}^{n-1}\) for point \(w^2\)
…
too big proofs, instead, we use the quotient polynomial to test many points at once, i.e., \(h(x)\) exists also means polynomial’s evaluation are 0 at the domain. In KZG, the quotient polynomial is the way to prove the evaluation of the polynomial, as the prover doesn’t know the evaluation point, thus the exist of quotient polynomial itself is to prove the polynomial’s evaluation. but here in IPA, it is not nessary as the verifier can choose the point and the prover prove the inner product is the evaluation.
So the main purpose of quotient polynomial in IPA is to combine many proofs to be one.
let’s assume there is a cheating prover, the polynomial constraint are not 0 when evaluated in the domain. which means \(h(x)\) is not a polynomial. but anyhow, pover will commit to something let’s say, prover make up a polynomial \(h'(x)\) and commit its coefficients \((c_0,c_1,…)\) using vector commitment. and verifier will choose a random point \(x\) to evaluate, which means prover need to generate the inner product proof of \((c_0,c_1,…)\) and \(1,x,x^2,…,x^{n-1}\), say it is \(v\). verifier then evaluate the polynomial constraint at \(x\), which means another IPA that prover need to prove, say\(y\), verifier compute vanish polynomial at \(x\) and get \(u\), then \(uv =y\) should holds, this with maximum possibility of \(\frac{d}{F}\)
multipoint opening argument
let’s talking about the example in Halo2 book

in this step, verifier need to check \(h(x)\)

how exactly?
as the prover already send the evaluations of \([A_0(x),…,H_{d-1}(x)]\) at point \(x\), verifier can compute the \(gate_0(x)+…+y^i\cdot gate_i(x)\) and \(h(x)\) from the evaluations sent by the prover, then verifier also can computes \(t(x)\), check the blow equation holds.
$$h(x)=\frac{gate_0(x)+…+y^i\cdot gate_i(x)}{t(x)}$$
this step prove the exist of quotient polynomial, which means the constraint polynomial \(gate_0(x)+…+y^i\cdot gate_i(x)\) indeed evaluate at 0 on domain.
then verifier need to get the proof that the committed polynomial it received at the beginning, indeed evaluated correctly at \(x\), i.e. the consistency between the \(\textbf{A,H}\) and \(evals\)
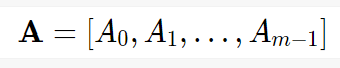

we of course don’t want to have IPA checks for all these polynomials. we want to combine them to one. How?
Intuition
To give a intuition of the design, let us think about we have two different polynomials, \(f(X)\) and \(g(X)\), prover sends the commitments of these two polynomials to verifier, and prover claim the evaluation of polynomials at \(z\) are \(y_1\) and \(y_2\), now we can combine these two polynomials to one IPA for opening:
by the homomorphsim of the commitment, verifier choose a random \(\alpha\) and combines the two commit by \(commit(f)+\alpha \cdot commit(g)\), and the new polynomial \(f(x)+\alpha\cdot g(x)\) evaluate at \(z\) should be \(y_1+\alpha y_2\), verifier ask the prover to open this new polynomial at \(z\) to verify.
in this case, if a prover cheats, say in truth \(f(z)=y_1’\) and \(g(x)=y_2’\), suppose the coefficients of \(f(x)\) is \(a_0,a_1,…,a_n\) and coefficients of \(g(x)\) is \(b_0,b_1,…,b_n\), then we have the new polynomial
$$(a_1+\alpha b_1)z+(a_2+\alpha b_2)z^2+…=y_1+\alpha\cdot y_2+$$
if the prover pass the check, which means
$$y_1’+\alpha y_2’= y_1+\alpha y_2$$
the only chance is luckily verifier choose \(\alpha = \frac{y_1-y_1′}{y_2′-y_2}\), the possibility is \(\frac{1}{F}\)
Halo2
the final poly is exactly following the above strategy

apart from, \(f(x)\) also combines polynomials evaluated at different point, i.e., \(wx, x\).