To understand the attack on Nova, I figure out I need to understand the role of the hash function and the validation check of hash function in Nova, from the first paper where the “cycle of curves” is not introduced, the circuit is illustrated as

to the circuit that has cycle of curves in the revisiting paper https://eprint.iacr.org/2023/969.pdf

The hash function in Nova
Recall the folding for a committed relaxed R1CS, the steps that both verifier and prover will do include
$$\bar{E}\leftarrow \bar{E}_1 + r\cdot \bar{T} + r^2 \cdot \bar{E}_2$$
$$s \leftarrow s_1 + r \cdot u_2$$
$$\bar{W} \leftarrow \bar{W}_1 + r \cdot \bar{W}_2$$
$$x \leftarrow x_1 + r \cdot x_2$$
for two committed relaxed R1CS \((\bar{E}_1,s_1,\bar{W}_1,x_1)\) and \((\bar{E}_2,s_2,\bar{W}_2,x_2)\). The relaxed R1CS structure is \(A Z\circ B Z=sCZ+E\), in the original paper, it is “\(uCZ+E\)”. I use “\(s\)” instead of “\(u\)”. As in the circuit, \(u\) is also the notation for committed relaxed R1CS.
Recall, \(x\) in the instance is the public input.
Given a folding scheme, let’s build a IVC proof from scratch. Intuitively, the first attempt is
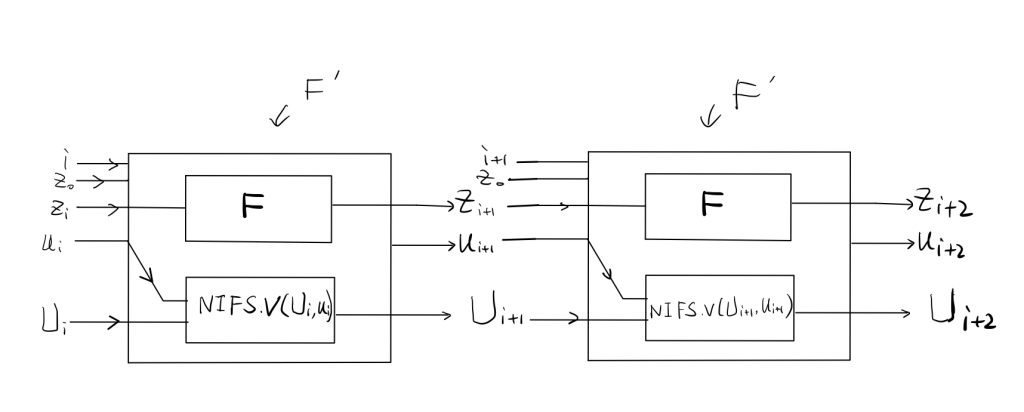
\(u_{i+1}\) is the proof for the execution of \(F’\), which includes two parts, as describe in the paper

these two are the statements.
The first problem comes, what are the public inputs and outputs for \(F’\)? i.e., \(u_i.x\)? It worth to mention that these public inputs and outputs are only for function \(F’\), for the SNARK prover at the end, it has different public inputs and outputs. The SNARK prover only takes the output of the last iteration of \(F’\) and compute the proof of the whole IVC based on that. SNARK prover doesn’t need to see the inputs and outputs of previous iterations of \(F’\). Therefore, there must be an mechanism embedded in the design that make sure the values transferred from one iteration of \(F’\) to next iteration of \(F’\) are correct. To figure out this mechanism, the first question is figure out what values are considered as public for \(F’\)
We consider the public inputs and outputs of the \(i+1\)th iteration of \(F’\), there are in total 8 values in the inputs and outputs of \(F’\):
$$i, z_0,z_i, u_i,U_i, z_{i+1}, u_{i+1}, U_{i+1}$$
let’s explore how many of them we need.
Case 1: only \((i,z_0,z_{i+1})\) are the public inputs.
in this case, \(u_{i+1}.x=(i,z_0,z_{i+1})\), prover can randomly choose \(z_i\), generate \(u_{i+1}\), let \(u_i= \perp\) or \(U_i=\perp\), prover can pass the SNARK verifier for iteration \(i+1\) with state \(z_{i+1}=F(z_i)\).
You may observe the reason this doesn’t work is that \(z_i\) and \((u_i,U_i)\) are not bonded together, giving the freedom to the attacker of choosing random \(u_i,U_i\).
The solution is simple, we need to bonded these values. How? recall that \(u_i\) itself has a public part, we add the values we want to bind together inside and add a validation check in \(F’\).
Case 2: \(i,z_0,z_{i+1},u_i,U_i\) are the public inputs
In this case, \(u_i\) itself has a pubic input part, and it should look like \(u_i.x=(i,z_0,z_{i},u_i, U_i)\)
The validation check follows the procedures below
\(F’\) take public inputs \(i,z_0,z_i,u_i,U_i\), compare them with the values in \(u_i.x=(i,z_0,z_1,z_i,U_i\), if values math, that means \(F’\) in \(i+1\)th iteration take the output from a valid \(i\)th iteration \(F’\) as inputs. This reasoning is recursive, until we can prove the whole chain is valid.
There is another problem as mentioned in the paper, the \(i+1\)th iteration of \(F’\) need to fold \(u_i\) and \(U_i\), but we see \(U_i\) is already included in \(u_i.x\), they have different size. To make this consistent, the hash function is introduced here.
Summary
From the above description, I conclude that, the hash function is to make \(U_i\) and \(u_i\) fold-able, because of the introduction of the hash function, the validation check become the format like now.
This make me think, is there any other way to do the validation check, but still keep \(u_i\) and \(U_i\) fold-able? This question is beyond the topic of this post series. In next post, I will discuss the attack on NOVA with the cycle of curves.