STARK 101 coding note

resource

low degree polynomials extension

interpolate the trace points into a polynomial in a small domain, then extend the domain, evaluate the interpolated polynomial into the bigger domain

Prime Field: a field created by module a prime number, remove 0 from it, then it is a cyclic group, a multiplicative group
the order of the group is p-1
any subgroup has an order that divides p-1

The trace polynomial needs to be evaluated on a larger domain to create a reed-solomon code

How to generate a group of order k in a prime field of order p-1?

Key: when \(k\) divides \(|\mathbb{F}^\times|\), \(g^k\) generates a group of size \(\frac{\mathbb{F}^\times|}{k}\)

If I want to generate a group of order \(k\)
– find a group generator \(g\)
– \(g^{\frac{\mathbb{F}^\times|}{k}}\) will generate the group we want

How to extend the group to be of order \(8k\), for example?
-find a group \(H\) with generator \(g^{\frac{\mathbb{F}^\times|}{8k}}\)

-Multiply each of the the elements in \(H\) with the generator of \(\mathbb{F}^\times\)

Correction of your illumination

polynomial evaluated in a small domain at the beginning

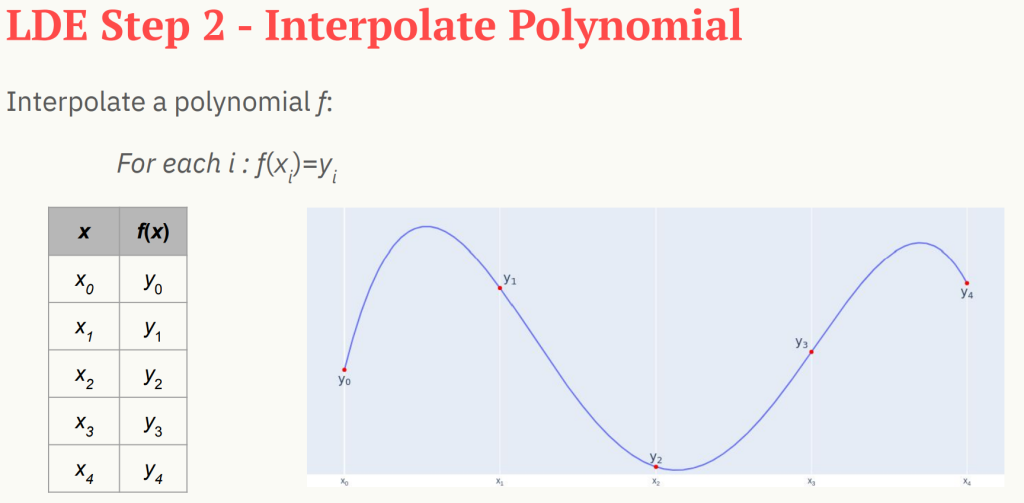
polynomial evaluated in the extended domain, it is more like interpolating more points between, instead of evaluating the polynomials in more points afterwards

note: polynomial in the pictures are lines for illumination purpose, in real they are not because the polynomial will modular \(p\)

send merkle tree root, the leaves are evaluations of the polynomial in this large domain

Polynomial Constrains

Start by specifying the constraints we care about (the FibonacciSq constraints).
Translate the FibonacciSq constraints into polynomial constraints.
Translate those into rational functions that represent polynomials if and only if the original constraints hold.

Rational functions:
Rational functions are functions that can be expressed as the ratio of two polynomial functions. In other words, a rational function 
f(x)=a(x)/b(x)

commit to the composition polynomial

The composition polynomial is already a combination of the quotients polynomials

FRI Commitment

The proof

what are committed:

decommitment

collection of your illumination

some resources talk about repeat the FRI protocol many rounds to get the desirable security level, some resources talk about get enough query points to get enough security level

Table of Contents